神经网络微分方程 (Neural ODEs)

本文转载：DiffEqFlux.jl – Julia 的神經微分方程套件

最近大半年都在思考怎么将水处理模型 (ASM, activated sludge model) 和机器学习 (ML, machine learning) 结合，也就是所谓的混合模型 (Hybrid model)。这是一个机会，目前水处理中应用的不是很多，代表性的大体有这么两篇：

• Hybrid differential equations: Integrating mechanistic and data-driven techniques for modelling of water systems
• An Integrated First Principal and Deep Learning Approach for Modeling Nitrous Oxide Emissions from Wastewater Treatment Plants

连续混合很简单，一个模型的输出作为另一个输出就好了。相比连续混合，我更喜欢的是并行混合，可玩性更高，下面给出公式表达：

Mechanistic ODE model:

\[ \frac{\mathrm{d} X(t)}{\mathrm{d} t} = f\left(X(t);p\right) \tag{1}\]

Neural ODE model:

\[ \frac{\mathrm{d} X(t)}{\mathrm{d} t} = n\left(X(t);w\right) \tag{2}\]

Hybrid ODE model:

\[ \frac{\mathrm{d} X(t)}{\mathrm{d} t} = f\left(X(t);p\right) + n\left(X(t);w\right) \tag{3}\]

公式很简单，想法很奇妙，无论在数学上，还是在专业机理上都能解释的通。机理模型负责解释，机器学习模型负责抓捕前者无法表达的信息。下面给出 Julia 官网上关于神经网络微分方程的文章，详细解释了该方向的理念。

1 神经微分方程库简介

Neural Ordinary Differential Equations 在这篇文章得到 NeurIPS 2018 的最佳论文奖的殊荣之前，其早已成为热门话题。这篇论文给出了许多令人赞赏的结果，它结合了两个不相干的领域，但这只不过是个开始而已： 神经网路与微分方程简直天生绝配。这篇部落格文章来自 Flux 套件的作者与 DifferentialEquations.jl 套件作者的合作，实作 Neural ODEs 论文, 将会解释为什么这个方向会诞生，以及这个方向现在和未来的走向， 也会开始描绘极致的工具会有怎样的可能性。

Julia 中运行树枝方法来解微分方程的 DifferentialEquations.jl 第三方库的众多优势已经在其他文章中详细讨论，除了经典Fortran方法的众多性能评测外，它包含了很多其它新颖的功能，像是 GPU 加速，分布式并行运算以及精密的事件处理。最近，这些 Julia 土生土长的微风方程方法已经成功地整合进 Flux 深度学习套件，并允许在神经网络中使用整套完整测试，优化的 DiffEq 方法。我们将会使用新套件 DiffEqFlux.jl展示给读者，在神经网络中增加微分方程层有多么简单，并可以使用一系列微分方程方法，包含刚性 (stiff) 常微分方程、随机微分方程、延迟微分方程以及混合微分方程。

这是第一个完美结合微分方程方法及神经网络模型的套件，能够融合神经网络和 ODEsm, SDEsm, DAEs, DDEs, 刚性方程，以及像伴随敏感度运算 (adjoint sensitivity calculations) 这样不同的方法，这是一个神经微分方程重大的广义话工作，将来提供更好的工具让研究者去安锁问题领域。

2 微分方程究竟与神经网络有何关联

对于不熟悉相关领域的人来说，想必第一个问题自然是：为什么微分方程在神经网络这个脉络下，会有举足轻重的关联？简而言之，微分方程可以借由数学模型来叙述，编码先验的结构化假设，来表示任何一种非线性系统。

让我们稍微解释下这句话在说什么。一般来说，主要有三种方法来定义一个非线性转换：

• 直接数学建模
• 机器学习
• 微分方程

直接数学建模可以直接写下输入与输出间的非线性转换，但只有在输入与输出间的函数关系形式为已知时可用，然而大部分的状况，两者间的确切关系并不是事先知道的，所以大多数问题是，你如何在输入和输出间的关系未知情况下，来对其做非线性数学建模？

其中一种解决方法是使用机器学习算法。典型的机器学习处理的问题里，会给定一些输入资料 \(x\) 和想要预测的输出 \(y\)，而由给丁 \(x\) 产生预测值 \(y\) 就是一个机器学习模型。在训练阶段，我们想办法调整 ML 的参数让它产生更正确的预测值。接下来，我们即可使用 ML 进行推论。同时，这也不过是一个非线性转换而已 \(y = \mathrm{x}\)。但是 ML 有趣的地方在于它本身数学模型的形式可以非常基本但却可以调整适应至各种资料。比如，一个简单的以 sigmoid 函数作为激活函数的神经网络模型，本质上来说就是简单的矩阵运算复合带入 sigmoid 函数里。相关机器学习理论已经保证了这是一个估计非线性系统的好办法，且 Universal Approximation Theorem 说明了只要有足够的层数或者参数，\(\mathrm{ML}(x)\) 可以逼近任何非线性函数。

这太好了，它总是有解！然而有几个需要注意的地方吗主要在于这个模型需要直接从资料里学习非线性转换。但是在大多数状况下，我们并不知道实际的非线性方程整体，但是我们却可以知道它的结构细节。举例来说，这个非线性转换可以是关于森林里兔子的数量，而我们可能知道兔子群体里的出生率正比于其数量。因此，与其从无到有去学习兔子群体数量的非线性模型，或许我们希望能够套用这个数量与出生率的先验关系，和一组参数来描述它。对于我们的兔子群体模型来说，可以写成：

\[ \mathrm{rabbits(tomorrow) = Model(rabbits(today))} \tag{4}\]

在这个例子里，我们得知群体出生率正比于群体数量这个先验知识，而如果用数学的方式去描述这个关于兔子群体大小结构的假设，即是微分方程。在这里，我们想描述的时间准确地说，是在给定的某一时间点的兔子群体的出生率将会随着兔子群体大小的增加而增加。简单地写的话，可以写成以下式子：

\[ \mathrm{rabbits}^{'}(t) = \alpha \cdot \mathrm{rabbits}(t) \tag{5}\]

其中，\(\alpha\) 可以是学习调整的参数。如果还记得微积分，这个方程的解即为成长率为 \(\alpha\) 的指数成长函数：

\[ \mathrm{rabbits}(t_\mathrm{start})e^{\alpha t} \tag{6}\]

值得注意的是，我们不需要知道这个微分方程的解才能验证以下想法：我们只需要描写模型的结构条件，数学即可帮助我们求解出这个解应该有的样子。基于这个理由，使得微分方程成为许多科学领域的工具。

但在近十年这些应用已经有了长足的发展，随着像是系统生物学 (system biology) 领域的发展，整合已知的生物结构以及数学上列举的假设，以学习到关于细胞间的交互作用，或是系统药理学 (system pharmacology) 中借由对一些特定药物剂量 PK/PD 建模。

所以随着我们的机器学习模型成长，会渴求更多更大量的资料，微分方程因此成为一个很有吸引力的选项，用以指定一个可学习但又有限制条件的非线性转换。他们会是在整合基友结构关系的领域知识，以及输入输出之间很重要的一个方式。有这个方法跟观点来看待两者，两个方法都有其需要取舍的优缺点，可以让彼此成为建模上互补的方法，这看起来是一条开始将科学实践与机器学习两者结合的明确道路，期待未来会有崭新而令人兴奋的未来！

3 什么是神经微分方程

神经微分方程只是众多结合这两个领域的方法之一。最简单的解释方法就是，并不是直接去学非线性转换，我们希望学到非线性转换的结构。如此一来，不用去计算 \(y=\mathrm{ML}(x)\)，我们将机器学习模型放在导数项上 \(y^{'}=\mathrm{ML}(x)\)，然后我们解微分方程。为什么要这么做呢？这是因为，一个动机就是定义这样的模型，然后用最简单，最容易出错的方式，欧拉法解微分方程，此时会得到一个跟残差神经网络 (residual nerual network)等价的结果：

\[ \Delta y = (y_{next} - y_{prev}) = \Delta x\cdot \mathrm{ML} (x) \tag{7}\]

即：

\[ y_{i+1} = y_i + \Delta x\cdot \mathrm{ML} (x_i) \tag{8}\]

这在结构上相似于 ResNet，最为成功的影像处理模型之一。Neural ODEs 论文的洞见就是，更加深，更加强大的类 ResNet 的模型可以有效地逼近类似于无限深，如同每一层接近于零的模型。我们可以直接建立微分方程，不投过增加层数这种手段，随后用特制的微分方程方法求解。

4 怎么解微分方程

首先，要如何解出微分方程的数值解呢？在 Julia 中可参考 ODE Problems，理解其中几个重要的参数：

• f：要求解的微分方程
• u0：变量初始状态
• tspan：要求解的时间区间
• p：要向微分方程中传递的参数
• kwargs：其它一些 keyword arguments

以经典的 Lotka-Volterra equations 为例：

\[ \begin{aligned} x^{'} &= \alpha x + \beta xy\\ y^{'} &= \gamma y + \gamma xy\\ \end{aligned} \tag{9}\]

写成 Julia 代码：

using DifferentialEquations
function lotka_volterra(du, u, p, t)
    x, y = u
    α, β, δ, γ = p
    du[1] = dx = α * x - β * x * y
    du[2] = dy = -δ * y + γ * x * y
end
u0 = [1.0, 1.0]
tspan = (0.0, 10.0)
p = [1.5, 1.0, 3.0, 1.0]
prob = ODEProblem(lotka_volterra, u0, tspan, p)
sol = solve(prob)
using Plots
plot(sol)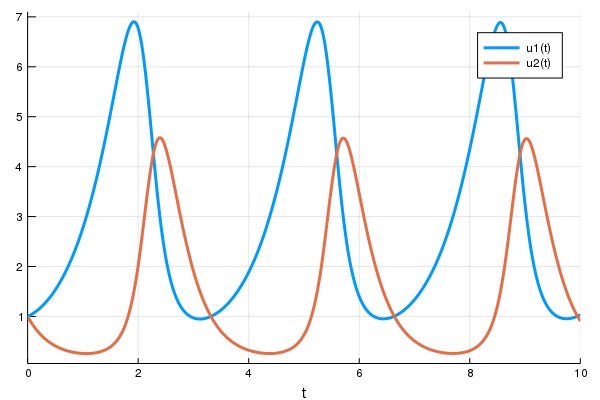

ODE

最后要说的是，可以让初始条件 (u0) 和时间段 (tspan) 成为参数 (p) 的函数，我们可以这样定义 ODEProblem：

u0_f(p, t0) = [p[2], p[4]]
tspan_f(p) = (0.0, 10 * p[4])
p = [1.5, 1.0, 3.0, 1.0]
prob = ODEProblem(lotka_volterra, u0_f, tspan_f, p)

如此一来，关于这个问题的所有东西都由向量 p 决定，这样写的好处会在后续章节显示出来。

5 微分方程放到神经网络框架

要理解一个微分方程方程是怎么被嵌入到一个神经网络中，那我们就要看看一个神经网络实际上是什么。一个层实际上就是一个可微分函数，它会吃进去一个大小为 n 的向量，然后吐出一个大小为 m 的新向量。就这样！网络层传统上就是简单的函数，像是矩阵相乘，但有了可微分方程的精神，人们越来越倾向于实验复杂的函数，像是光线追踪以及物理引擎。

恰巧微分方程方法也符合这样的架构，一个方法会吃进某个向量 p，然后输出某个新向量，也就是解。而且它还是可微分的，这代表我们可以直接把它推进大型可微分方程内。这样大型方程可以开心地容纳神经网络，以及我们可以继续使用标准最佳化技巧，像是 ADAM 来最佳化权重。

DiffEqFlux.jl 让这件事做起来非常简单：

p = [1.5, 1.0, 3.0, 1.0]
prob = ODEProblem(lotka_volterra, u0, tspan, p)
sol = solve(prob, Tsit5(), saveat=0.1)
A = sol[1, :] # length 101 vector

plot(sol)
t = 0:0.1:10.0
scatter!(t, A)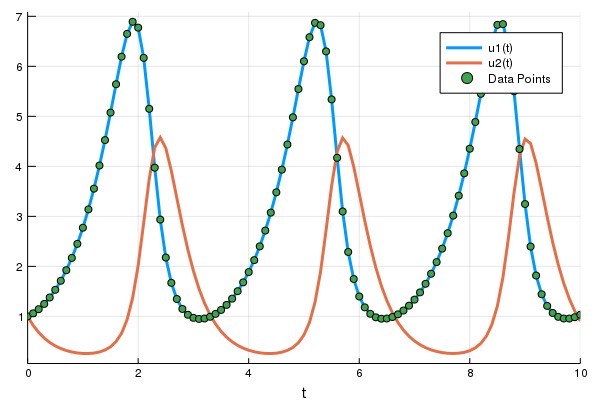

Nerual ODE

在 solve 中的一个好的设计就是，它会处理型别的相容性，让它可以相融于神经网络框架 (Flux)。要证明这点，我们定义一层神经网络，然后还有损失函数：

p = [2.2, 1.0, 2.0, 0.4] # 初始參數向量
params = Flux.params(p)

function predict_rd() # 我們的單層神經網路
    solve(prob, Tsit5(), p=p, saveat=0.1)[1, :]
end

loss_rd() = sum(abs2, x - 1 for x in predict_rd()) # 損失函數

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () # 用 callback function 來觀察訓練情況
    display(loss_rd())
    # 利用 `remake` 來再造我們的 `prob` 並放入目前的參數 `p`
    display(plot(solve(remake(prob, p=p), Tsit5(), saveat=0.1), ylim=(0, 6)))
end

# 顯示初始參數的微分方程
cb()
Flux.train!(loss_rd, params, data, opt, cb=cb)

Flux 在寻找可以最小化损失函数的神经网络参数 p，也就是说它会训练神经网络：在神经网络中向前传递的过程也包含了解微分方程的过程，当损失函数会惩罚当兔子数量远离 1 的时候，所以神经网络会找到兔子以及狼的群组都是常数 1 的时候的参数。

微分方程作为一层网络解完了，也可以随意将它加到任何地方。举例而言，多层感知机 (multilayer perceptron) 可以用 Flux 写成：

m = Chain(
    Dense(28^2, 32, relu),
    Dense(32, 10),
    softmax)

而且，假设我们带有合适大小的参数向量 ODE，可以将其代入到模型中：

m = Chain(
    Dense(28^2, 32, relu),
    # this would require an ODE of 32 parameters
    p -> solve(prob, Tsit5(), p=p, saveat=0.1)[1, :],
    Dense(32, 10),
    softmax)

6 完整的 ODE 求解工具对于这个应用为什么是必须的

7 用 Julia 写作一个常微分方程神经网络

8 用范例理解常微分神经网络的行为

现在，让我们用一个例子来看看常微分神经网络到底是什么样子。首先，让我们用一个常微分方程来产生一个均匀时间点的时间序列：

u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 1.5f0)

function trueODEfunc(du, u, p, t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u .^ 3)'true_A)'
end
t = range(tspan[1], tspan[2], length=datasize)
prob = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob, Tsit5(), saveat=t))

dudt = Chain(x -> x .^ 3,
    Dense(2, 50, tanh),
    Dense(50, 2))
n_ode = NeuralODE(dudt, tspan, Tsit5(), saveat=t, reltol=1e-7, abstol=1e-9)
ps = Flux.params(n_ode)

注意到 Neural ODE 中使用的常微分方程解相同的时间跨度和 saveat，所以会在每个时间点针对神经网络预测的动态系统状态产生一个预测值。让我们来看看这最初的神经网络会给出什么样的时间序列。下面只给出其中第一个变量变化：

pred = n_ode(u0) # 使用真實的初始值來產生預測值
scatter(t, ode_data[1, :], label="data")
scatter!(t, pred[1, :], label="prediction")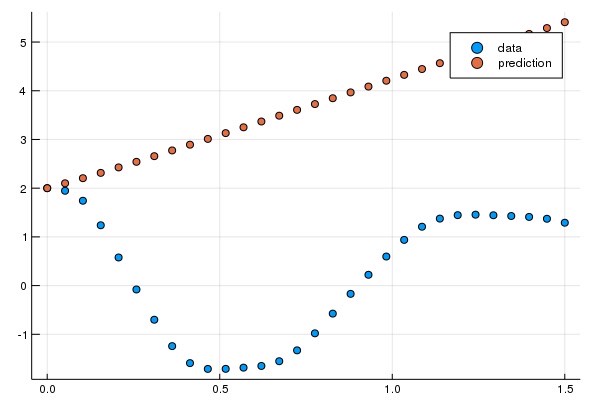

Neural ODE

开始训练：

function predict_n_ode()
    n_ode(u0)
end
loss_n_ode() = sum(abs2, ode_data .- predict_n_ode())

data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () # 觀察資料用的 callback 函數
    display(loss_n_ode())
    # 畫出當下預測和資料
    cur_pred = predict_n_ode()
    pl = scatter(t, ode_data[1, :], label="data")
    scatter!(pl, t, cur_pred[1, :], label="prediction")
    display(plot(pl))
end

# 呈現初始參數下的常微分方程
cb()

Flux.train!(loss_n_ode, ps, data, opt, cb=cb)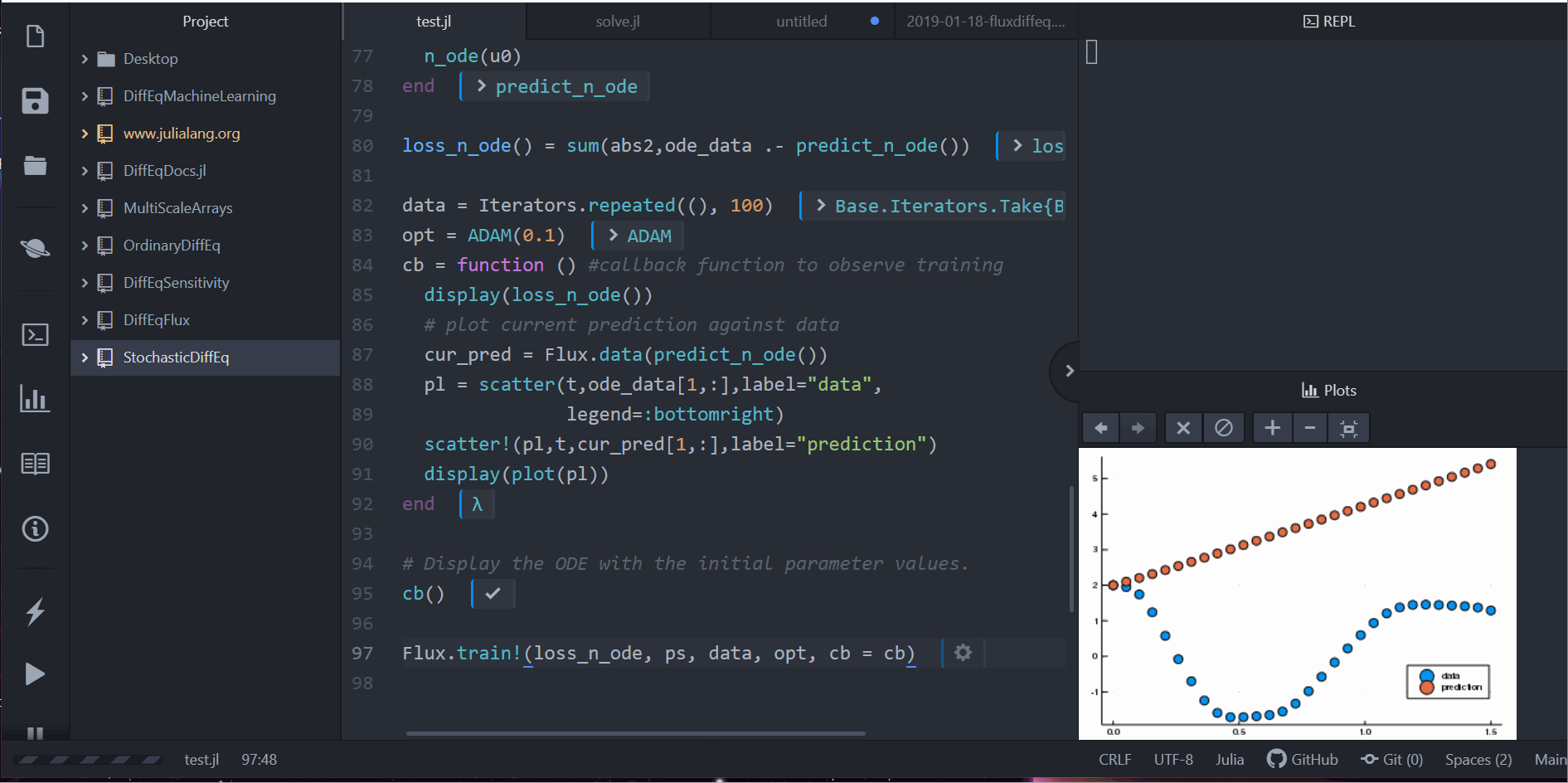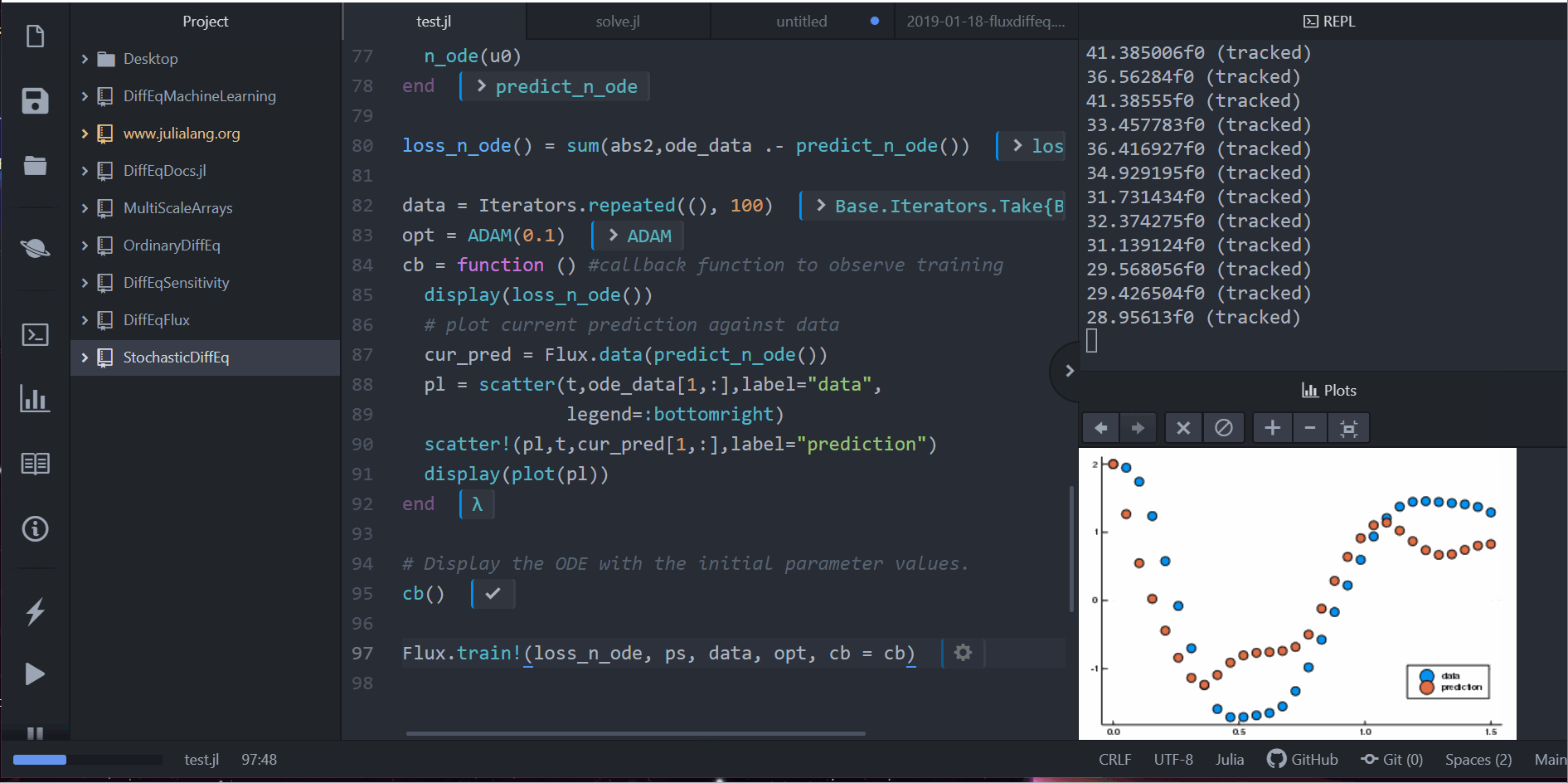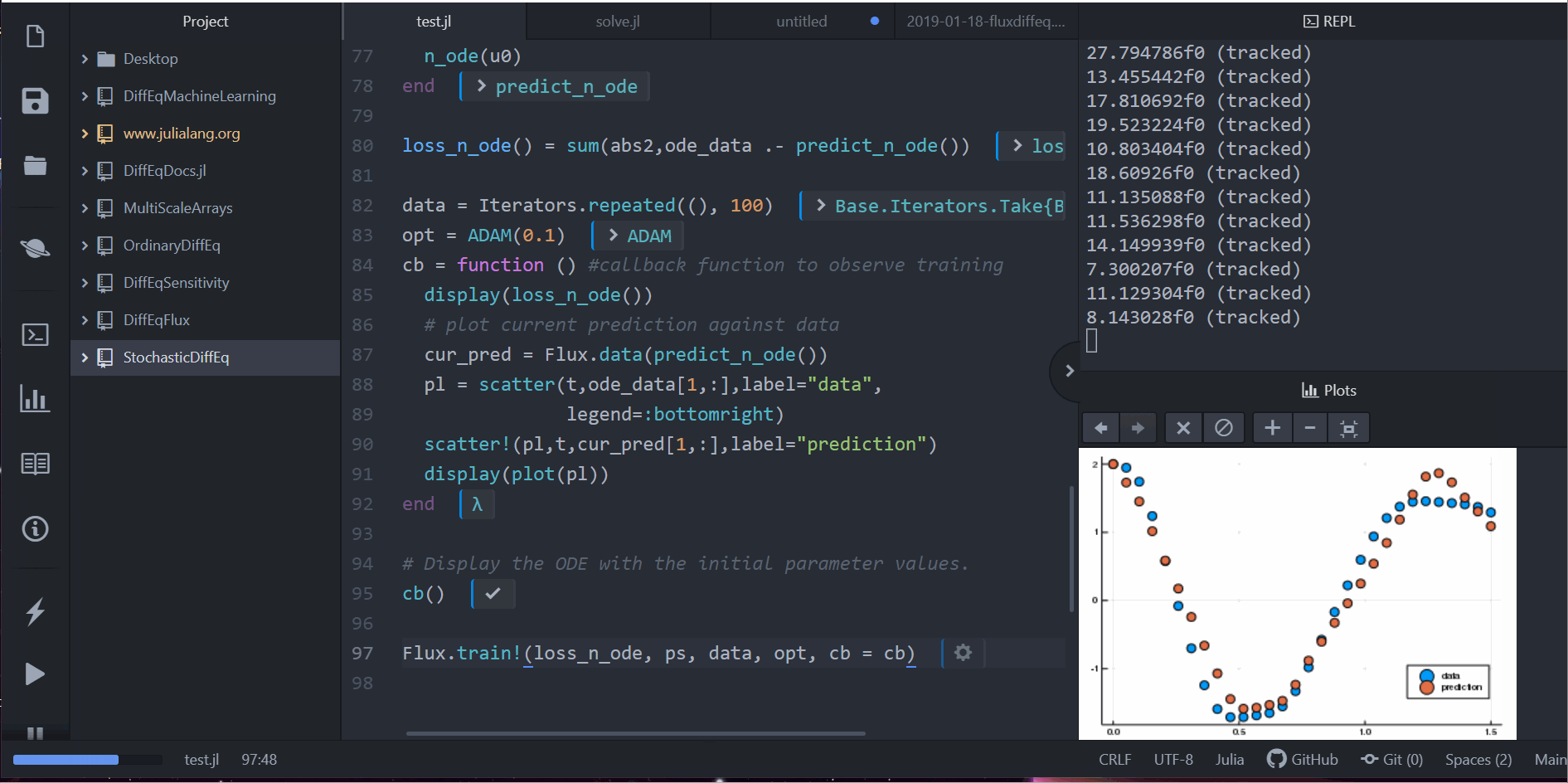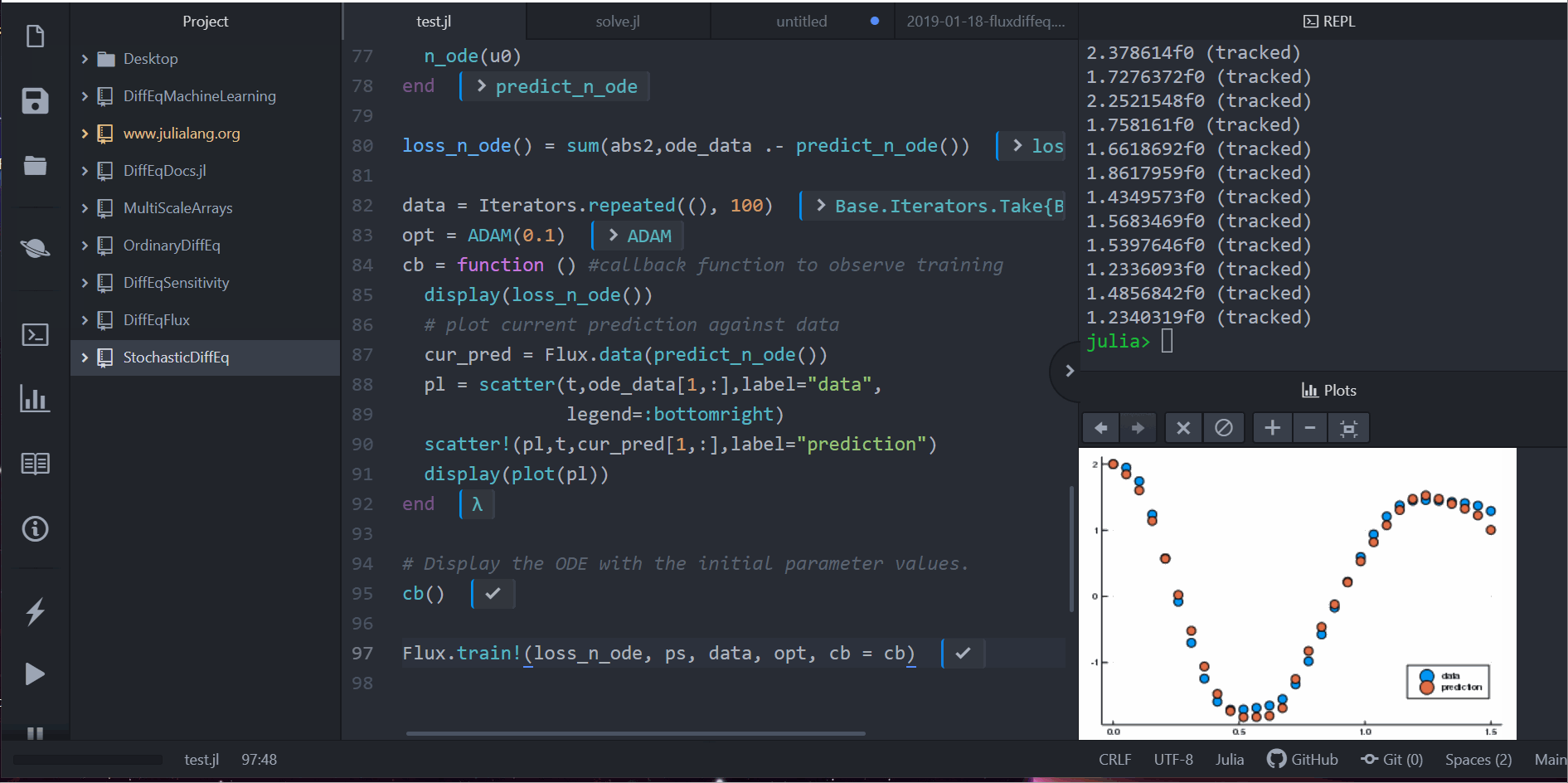

Neural ODE 训练过程

注意到，我们并不是针对 ODE 的解去学习，而是学习一个可以产生这组解的小小 ODE 系统。也就是说，这个在 Neural ODE 中的神经网络学到的是这样一个函数：

学到的是这组时间序列如何运作的一个完整的表示法，并且可以轻易的使用不同的初始条件对接下来的值进行外插。除此之外，这是个可以学习这样的表示法非常弹性的架构。举例来说，如果数据集中有的不是均匀间隔的时间点 t，只需要在 ODE 计算中让 saveat=t，让其去处理这个问题即可。